Publicación Científica de la Universidad de Ciencias Médicas de Ciego de Ávila                          Editorial Ciencias Médicas
	REVISTA MÉDICA ELECTRÓNICA DE CIEGO DE ÁVILA	2022;28:e3471 ISSN: 1029-3035 RNPS: 1821

Artículo original

Aplicación del algoritmo del bosque aleatorio a un modelo de clasificación de la anemia en niños peruanos

Application of the random forest algorithm to a model of anemia classification in Peruvian children

Bernardo Céspedes-Panduro^1,2* https://orcid.org/0000-0002-9606-1478

¹Universidad Nacional Mayor de San Marcos. Lima, República del Perú.
²Universidad Nacional del Santa. Ancash, República del Perú.

*Autor para la correspondencia. Correo electrónico: bcespedesp@unmsm.edu.pe

RESUMEN
Introducción: en el Perú, durante los últimos años se observa una disminución de la pobreza. No obstante, la prevalencia de anemia continúa alta; afecta a 40,00 % de los niños de seis a 35 meses de edad.
Objetivo: identificar los factores de riesgo o pronósticos en la aparición de anemia en niños peruanos.
Métodos: se realizó un estudio observacional transversal a partir de la base de datos creada para la Encuesta Demográfica y de Salud Familiar, por el Instituto Nacional de Estadística e Informática durante los años 2015-2019. La población estuvo constituida por 57 410 niños de seis a 35 meses de edad, que contaban con exámenes de hemoglobina. Se seleccionaron 33 variables independientes y se plantearon seis procedimientos con el algoritmo del bosque aleatorio. Se obtuvieron valores de los indicadores área bajo la curva, especificidad y sensibilidad.
Resultados: el procedimiento que mejor predijo la presencia de anemia, con valores para los indicadores de especificidad (63,62 %) y sensibilidad (65,88 %) más similares, utilizó datos balanceados con reajuste de los parámetros, reducción de la cantidad de árboles y selección de variables.
Conclusiones: las cinco variables independientes más importantes para el modelo fueron: edad del niño, altitud del conglomerado, número de visitas prenatales por embarazo, momento del primer control prenatal y talla de la madre. El estudio aportó evidencias científicas acerca del uso de los algoritmos de aprendizaje automático para predecir la aparición de anemia en función de factores de riesgo comunes.
Palabras clave: ANEMIA; ANEMIA/PREDICCIÓN; ALGORITMOS; ÁREA BAJO LA CURVA; SENSIBILIDAD Y ESPECIFICIDAD; NIÑO.

ABSTRACT
Introduction: in Peru, in recent years there is a decrease in poverty. However, the prevalence of anemia continues high; it affects 40,00 % of children from six to 35 months of age.
Objective: to identify risk factors or forecasts in the appearance of anemia in Peruvian children.
Methods: a transverse observational study was carried out from the database created for the Demographic and Family Health Survey, by the National Institute of Statistics and Informatics during the years 2015-2019. The population was constituted by 57 410 children from six to 35 months of age, which had hemoglobin exams. 33 independent variables were selected and six procedures were raised with the random forest algorithm. Values of the area indicators under the curve, specificity and sensitivity were obtained.
Results: The procedure that best predicted the presence of anemia, with values for specificity indicators (63,62 %) and sensitivity (65,88 %) more similar, used balanced data with readjustment of the parameters, reduction of the amount of trees and selection of variables.
Conclusions: the five most important independent variables for the model were: child age, conglomerate altitude, number of prenatal visits for pregnancy, moment of the first prenatal control and size of the mother. The study provided scientific evidence about the use of automatic learning algorithms to predict the appearance of anemia based on common risk factors.
Keywords: ANEMIA; ANEMIA/FORECASTING; ALGORITHMS, AREA UNDER CURVE; SENSITIVITY AND SPECIFICITY; CHILD.

Recibido: 24/03/2022
Aprobado: 31/05/2022

INTRODUCCIÓN

En el Perú, durante los últimos años se observa una disminución de la pobreza. No obstante, la prevalencia de anemia continúa alta; afecta a 40,00 % de los niños de seis a 35 meses de edad.⁽¹⁾ A nivel departamental, la mayor frecuencia se localiza en Puno (69,40 %), seguido por Ucayali (57,20 %) y Madre de Dios (55,00 %); y la menor, en Tacna (29,20 %). La región natural con mayor porcentaje de anemia es la sierra (48,50 %), seguida por la selva (46,30 %). Asimismo, por área de residencia, el mayor porcentaje de niños anémicos se encuentra en el área rural (48,40 %).⁽¹⁾

Debido al impacto que ocasiona esta enfermedad en la salud de las personas y en la sociedad, en el año 2017 se aprobó en el país el "Plan nacional para la reducción y control de la anemia materno infantil y desnutrición crónica infantil 2017-2021",⁽²⁾ donde se priorizaron intervenciones preventivas en niños menores de tres años.

En el año 2018 el gobierno elaboró el Plan multisectorial de lucha contra la anemia,⁽³⁾ en el cual se definen acciones e intervenciones efectivas a ser implementadas de manera articulada, intersectorial e intergubernamental por las entidades del gobierno nacional, los gobiernos regionales y locales, así como por la sociedad civil y las comunidades organizadas, para prevenir y reducir la incidencia de la anemia en niños menores de 36 meses. Su implementación abarca a toda la población, con énfasis en los ámbitos priorizados (aquellos con mayores brechas de pobreza y anemia infantil).

Sin embargo, pese a todos los programas que implementa el Gobierno, la incidencia de la anemia aumenta, ya que: “es un problema estructural que se acentúa por las desigualdades económicas, sociales y culturales, que se manifiestan en pobreza, precariedad de las condiciones de la vivienda (en especial respecto del acceso a agua y saneamiento), desconocimiento de las familias sobre la importancia de la alimentación saludable y las prácticas de higiene, entre otros factores. Todo ello atenta contra el desarrollo integral de los niños y, por ende, contra el ejercicio de sus derechos en el presente y en el futuro”.⁽³⁾

La predicción mediante variables relacionadas con la salud del niño, la familia, el hogar y la comunidad es un aspecto importante en los esfuerzos por reducir las cifras de anemia. En 2012 Sanou y Ngnie-Teta⁽⁴⁾ propusieron un marco teórico nuevo para el análisis de los factores de riesgo de la anemia en niños en edad preescolar, el cual justifica el análisis por multiniveles. En este, las variables se definen jerárquicamente, especialmente las individuales, familiares y comunitarias.

En la literatura internacional se encuentran otros modelos causales de la anemia, como los de Balarajan y cols.⁽⁵⁾ (2011), Saaka y Galaa⁽⁶⁾ (2017), y Siekmans y cols.⁽⁷⁾ (2014). Entre las causas inmediatas de la afección se reconocen la carencia orgánica de hierro y otros micronutrientes a partir de una alimentación deficiente, lo cual dificulta la formación de los glóbulos rojos y la hemoglobina. Otras causas inmediatas de la anemia son la alta morbilidad por infecciones como diarreas, parasitosis, malaria, asociadas a prácticas higiénicas inadecuadas, acceso limitado al agua potable tratada y saneamiento básico.⁽⁸⁾

Las vitaminas A, B2, B6, B12 y el ácido fólico intervienen en la formación de los glóbulos rojos en la médula ósea. Las vitaminas A, C y riboflabina favorecen la absorción intestinal del hierro, y movilizan el mineral a partir de las reservas. Por otra parte, las vitaminas C y E tienen funciones antioxidantes, protectoras de los glóbulos rojos.⁽⁵⁾

En la actualidad el aprendizaje automático (machine learning) es vital para el análisis de datos. Su finalidad es dotar a una máquina, a través de algoritmos, de la capacidad de entrenar y aprender a partir de los datos. Ello, sin ser explícitamente programada, para lo cual imita la capacidad de las personas de aprender mediante ejemplos, sin recurrir a fórmulas ni reglas entre variables. De esta forma es posible, al término del entrenamiento, contar con un modelo para la generalización; es decir, obtener resultados durante el aprendizaje, en situaciones desconocidas.⁽⁹⁾

Ello posibilita resolver situaciones para las cuales no existe, o es muy difícil encontrar, una fórmula que genere respuestas exactas a partir del conocimiento de ciertas variables. El modelo podrá reconocer y clasificar nuevas imágenes si se ha "entrenado" en un conjunto de casos o ejemplos representados por determinadas características e imágenes correspondientes.⁽⁸⁾ Dentro de los algoritmos existentes están los árboles de decisión, los cuales conforman los bosques aleatorios para modelos de clasificación.⁽⁹⁾

Uno de los problemas más comunes en el ámbito de las ciencias sociales y las ciencias médicas es disponer de un buen método de clasificación de la variable respuesta (el niño tiene anemia, o no). Para etiquetar a un sujeto mediante ciertas características descriptivas –en dependencia del objetivo trazado– se necesita crear un buen modelo predictivo de clasificación de datos. En el caso particular de uno sobre la anemia infantil, deberá indicar probabilísticamente si el niño la padece o no, para que las instituciones sanitarias generen programas de prevención al efecto.

El objetivo de la presente investigación es identificar los factores de riesgo o pronósticos en la aparición de anemia en niños peruanos.

MÉTODOS

Se realizó un estudio observacional transversal. La población estuvo constituida por 57 410 niños de seis a 35 meses de edad de la República del Perú, que contaban con exámenes de hemoglobina. Los datos fueron recolectados a través de la Encuesta Demográfica y de Salud Familiar (ENDES), por el Instituto Nacional de Estadística e Informática (INEI), durante los años 2015 a 2019. Se descargaron del menú “Bases de Datos” de la página web del INEI (http://iinei.inei.gob.pe/microdatos/).

La variable respuesta es la aparición de anemia en niños de seis a 35 meses de edad, la cual se confirma cuando el valor corregido de la hemoglobina es inferior a 11 mg/dl.⁽¹⁰⁾ A partir de los modelos de Sanou y Ngnie-Teta⁽⁴⁾, Balarajan y cols.⁽⁵⁾, Saaka y Galaa⁽⁶⁾, y Siekmans y cols.⁽⁷⁾, las variables independientes se organizaron en tres grupos:

Sociodemográficas: área de residencia, altitud de la ciudad donde vive el niño, región natural, índice de bienestar o riqueza del hogar, edad materna, grado de instrucción de la madre, lengua materna de la madre, conexión domiciliaria de agua potable, conexión domiciliaria de desagüe, material predominante del piso de la vivienda.

Relacionadas con el niño: sexo, edad, número de niños menores de cinco años en el hogar, número de personas que viven en el hogar, bajo peso al nacer (<2 500 gr), orden de nacimiento, intervalo entre nacimientos, signos y síntomas (fiebre) en las dos semanas previas, diarrea durante las dos últimas semanas, tos y respiración rápida durante las dos últimas semanas.

Del cuidado materno e infantil: control prenatal, control prenatal en primer trimestre, parto institucional, talla de la madre, diagnóstico de anemia en la madre en el momento de la encuesta, tiempo de consumo de suplementos de hierro en la gestación, suplementos de vitamina A, si el niño recibió hierro en pastillas o jarabes, medicación antiparasitaria en el niño (tratamiento en los últimos seis meses), si el niño comió algún tipo de carne (res, pollo, hígado, cerdo, entre otros) el día anterior, consumo de agua hervida, y control de crecimiento y desarrollo.

Las bases de datos de la ENDES están organizadas por módulos de acuerdo al rubro de información. Se descargaron los módulos: RECH6, REC0111, RECH0, REC91, RECH23, RECH5, REC95, REC43 y REC41, que miden las características de la anemia en niños y madres, la salud infantil y materna, y las características sociodemográficas de hogares y viviendas.

Se realizó la imputación de los valores faltantes (perdidos) en la base de datos construida a partir de la ENDES, mediante la librería Hmisc del software estadístico R (versión 4.0.5) con su función aregImpute(). El algoritmo de imputación múltiple de Hmisc funciona de la siguiente forma: cada variable con datos perdidos, se inicializa con los valores de una muestra aleatoria de aquellos observados. A continuación, extrae una muestra de reemplazo del conjunto de datos completo, y ajusta un modelo aditivo flexible para predecir los valores de todos los casos. Finalmente, imputa cada dato faltante con el observado, cuyo valor predicho es más cercano al predicho del dato faltante (pareamiento por medias predictivas).⁽¹¹⁾

Se recategorizaron los valores de las variables independientes para mantener la estabilidad en el procedimiento alternativo propuesto. Las categorías de cada predictor se juntaron si no eran significativamente distintas respecto a la variable respuesta; para ello se utilizó la técnica de árboles de decisión CHAID (Chi-square automatic interaction detector) mediante el software estadístico R. Esta técnica identifica las divisiones óptimas y genera árboles no binarios (algunas divisiones generan más de dos ramas).

Se dividió la base de datos en dos partes: una de entrenamiento, que correspondió a su mayor parte (usada para entrenar el modelo) y otra de prueba, de menor tamaño (sobre la cual se evaluó el modelo entrenado). La división se hizo de forma aleatoria estratificada, basada en la variable respuesta, con ayuda de la librería entrenamiento de clasificación y regresión (caret) del software estadístico R.

En la aplicación del algoritmo del bosque aleatorio con el software estadístico R para predecir la anemia en niños de seis a 35 meses de edad, se tuvieron en cuenta seis procedimientos alternativos (A, B, C, D, E, y F). Estos se obtuvieron mediante la combinación de los criterios de balanceo de datos y el reajuste de los parámetros para la predicción de anemia:

Procedimiento A: se planteó sin que la variable respuesta estuviera balanceada; se consideraron todas las variables y se utilizaron, por defecto, los parámetros del algoritmo del bosque aleatorio.

Procedimiento B: se planteó la variable respuesta, balanceada. Se consideraron todas las variables y se utilizaron, por defecto, los parámetros del algoritmo del bosque aleatorio.

Procedimiento C: se planteó sin que la variable respuesta estuviera balanceada; se reajustaron los parámetros, mediante una búsqueda en rejilla, para encontrar los mejores y reducir la cantidad de árboles a 300, con todas las variables.

Procedimiento D: se balanceó la variable respuesta, para lo cual se efectuó un reajuste de los parámetros mediante una búsqueda en rejilla. De esa forma se encontraron mejores parámetros y se redujo la cantidad de árboles a 300, con todas las variables.

Procedimiento E: se planteó sin que la variable respuesta estuviese balanceada. Par ello, se reajustaron los parámetros mediante una búsqueda en rejilla. Esta posibilitó encontrar los mejores parámetros del algoritmo del bosque aleatorio, y se redujo la cantidad de árboles a 300, con variables seleccionadas.

Procedimiento F: se balanceó la variable respuesta, para lo cual se reajustaron los parámetros mediante una búsqueda en rejilla. De esa forma se encontraron los mejores parámetros del algoritmo del bosque aleatorio, y se redujo la cantidad de árboles a 300, con variables seleccionadas.

Para balancear la variable respuesta, se utilizó el método de combinación (both sampling) con ayuda de la librería “ROSE” del software estadístico R.

Se evaluaron los seis procedimientos alternativos propuestos con los indicadores: área bajo la curva, sensibilidad y especificidad mediante las librerías caret y bosque aleatorio del software estadístico R para saber cuál es el mejor procedimiento alternativo.

Por último, se calculó la importancia relativa de cada una de las variables mediante el procedimiento alternativo, para el cual se utilizó el coeficiente de Gini. Este consiste en el promedio (media) de la disminución total de la impureza del nodo de una variable, ponderada por la proporción de muestras que llegan a ese nodo en cada árbol de decisión individual en el bosque aleatorio. Un mayor coeficiente de Gini indica mayor importancia de la variable.

En enfoque del bosque aleatorio, se crea un gran número de árboles de decisión. Cada observación se introduce en un árbol de decisiones. El resultado más común para cada observación se utiliza como resultado global. Una nueva observación se introduce en todos los árboles, y toma el dato mayoritario para cada modelo de clasificación.

Las respuestas de los modelos de clasificación son variables cualitativas; se debe tener en cuenta que las variables independientes pueden ser cualitativas o cuantitativas, para predecir cualquiera de las dos categorías. Por ejemplo: predecir si un alumno aprobará o no, si un niño tendrá o no anemia. Estos modelos utilizan la tabla de clasificación de Fernández-Vázquez,⁽¹²⁾, cuyas distribuciones de valores observados y pronosticados son las siguientes:

Sensibilidad: indica la capacidad de un modelo para clasificar correctamente la categoría de interés de la variable respuesta.

Especificidad: indica la capacidad de un modelo para clasificar correctamente la categoría que no es de interés de la variable respuesta.

Área bajo la curva: mide el área debajo de la curva característica operativa del receptor (ROC, por receiver operating characteristic) para comparar clasificadores. Un clasificador perfecto tendrá un área debajo de la curva ROC igual a uno, mientras que un clasificador puramente aleatorio la tendrá igual a 0,5. Según Pérez-Sánchez y cols.⁽¹³⁾ la diagonal principal corresponde a la peor prueba de diagnóstico, y tiene un área bajo la curva de 0,5.

Este estudio estuvo exento de aprobación ética porque se limitó a conjuntos de datos públicos, que no contenían información personal. Todos los participantes dieron su consentimiento informado a los entrevistadores de la ENDES antes de inscribirse en el estudio.

RESULTADOS

Procedimiento para la predicción de anemia

En la tabla 1, se observa un porcentaje alto (45,7%) de niños de seis a 35 meses de edad con anemia.

Tabla 1 - Distribución de la anemia en los niños

Se dividió la muestra aleatoria estratificada según la variable respuesta. Para observar el desempeño del modelo, tal como se muestra en la tabla 2, los datos se dividieron en 70 % para entrenamiento y 30 % para evaluación.

Tabla 2 - Distribución de la anemia en los niños según estratos

0: sin anemia; 1: con anemia

En la tabla 3 se muestra la clasificación de cada uno de los procedimientos alternativos. El porcentaje correcto de clasificación más alto (65,80 %) se obtuvo a partir del procedimiento A, seguido del C (65,37 %) y el E (65,31 %). Asimismo, con los procedimientos D y F se obtuvieron los porcentajes correctos más altos para pronosticar la anemia (63,62 % en ambos).

Tabla 3 - Tablas de clasificación de la prevalencia de anemia en niños según los procedimientos alternativos

0: sin anemia; 1: con anemia

En la tabla 4 se muestran los indicadores (área bajo la curva, especificidad y sensibilidad) de los procedimientos alternativos propuestos para el conjunto de datos de la evaluación.

Tabla 4 - Comparación de los indicadores de los procedimientos alternativos propuestos para los datos de la evaluación

Los seis procedimientos alternativos propuestos obtuvieron indicadores de área bajo la curva alrededor de 0,70. De acuerdo a las definiciones de Pérez-Sánchez y cols.,⁽¹³⁾ la calidad de predicción de los seis procedimientos alternativos fue regular.

En los resultados del indicador de especificidad existieron diferencias. Se evaluó la predicción sobre la categoría que no era de interés –en este caso, cero (sin anemia)– para los procedimientos alternativos D y F, para las cuales se obtuvieron valores mayores. Ello era esperable, puesto que el aprendizaje en los procedimientos alternativos planteados se limitó a la categoría de mayor frecuencia; es decir, sobre la categoría de los ceros (sin anemia) se encontraron los mejores parámetros del algoritmo del bosque aleatorio mediante la búsqueda en rejilla.

En los resultados del indicador de sensibilidad existieron diferencias; se evaluó la predicción de la categoría de interés –en este caso la uno (con anemia)–  y en los procedimientos alternativos A y C se obtuvieron valores mayores. Lo cual era esperable, puesto que la especificidad para estos procedimientos alternativos es baja; de ahí la necesidad de balancear la variable respuesta para que los procedimientos alternativos que se plantearon aprendieran de ambas categorías.

Identificación de las variables de acuerdo con su importancia

En el algoritmo del bosque aleatorio las variables con alta importancia tienen una fuerte asociación con los resultados de la predicción; ello constituye una de sus ventajas.

Para estimar la importancia de la variable para alguna variable j, las muestras fuera de la bolsa se pasan por el árbol y se registra la precisión de la predicción. Después, los valores de la variable j se permutan en las muestras fuera de la bolsa y la precisión se mide nuevamente. Estos cálculos se realizan árbol por árbol, a medida que se construye el bosque aleatorio. La disminución promedio en la precisión de estas permutaciones se calcula sobre todos los árboles, y se usa para medir la importancia de la variable j. La disminución sustancial de la precisión de la predicción, sugiere que la variable j tiene una fuerte asociación con la respuesta.⁽¹⁶⁾ Después de medir la importancia de todas las variables, el bosque aleatorio devolverá una lista clasificada de la importancia de la variable.

Formalmente, sean β_t las muestras fuera de la bolsa para el árbol t, t ∈ {1, ..., n árbol}, y'^t_i es la clase predicha para la instancia i antes de la permutación en el árbol t y y'^t_i,α es la clase predicha por ejemplo i después de la permutación. La importancia de la variable (VI, por variable importance) para la variable j en el árbol t viene dada por:

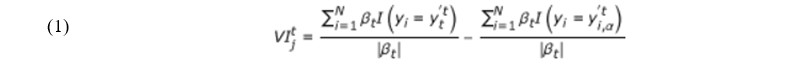
El valor de importancia sin procesar para la variable j se promedia sobre todos los árboles en el bosque aleatorio.

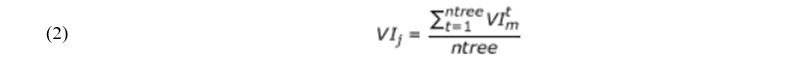
La variable utilizada es el coeficiente Gini de disminución media, basado en el criterio de división de Gini. Los coeficientes Gini de disminución media miden la disminución ΔI resultante del desdoblamiento. Para un problema de dos clases, el cambio en I (ecuación 4) en el nodo t se define como la impureza de clase (ecuación 3) menos el promedio ponderado de la medida de Gini.⁽¹⁴⁾

La disminución en la impureza de Gini se registra para todos los nodos t en todos los árboles (n árbol) en el bosque aleatorio, para todas las variables. Después se calcula la importancia de Gini (GI, por Gini importance)^(14-16) como:

En la tabla 5 se observa la importancia de cada una de las cinco variables más importantes para cada procedimiento alternativo, con su indicador de importancia relativa.

Tabla 5 - Nivel de importancia de las cinco variables con mayor puntaje según los procedimientos alternativos empleados

Mediante el algoritmo del bosque aleatorio y el indicador del coeficiente de Gini se determinaron las cinco variables de importancia relativa para los procedimientos alternativos. Las cuales son: edad del niño (en meses), altitud del conglomerado (en metros), visitas prenatales por embarazo, momento del primer control prenatal y talla de la madre (en centímetros). Estas variables se deben tener en cuenta para el lanzamiento de futuras políticas públicas encaminadas a la disminución del porcentaje de niños con anemia.

DISCUSIÓN

Estos resultados son comparables con los del estudio de Khan y cols.⁽¹⁷⁾ en 2019, quienes constataron con el mismo algoritmo del bosque aleatorio una sensibilidad de 70,73 %, una especificidad de 66,41 % y un área bajo la curva de 0,6857.

La integración de técnicas de aprendizaje automático para predecir la supervivencia del paciente y el estado de la enfermedad, es frecuente en las investigaciones de salud pública.^(17-19) Ello impacta de forma positiva en la mejora de la planificación de la atención médica. Sin embargo, hasta la fecha, se han realizado muy pocas investigaciones sobre el uso de algoritmos de aprendizaje automático para predecir el estado de la enfermedad mediante datos de encuestas de salud y demográficas transversales.^(20,17) Además, ninguna investigación ha explorado el potencial del bosque aleatorio para predecir el estado de anemia de los niños de seis a 35 meses en Perú a partir de la ENDES. En el presente estudio se constató que es posible predecir con precisión la anemia infantil a partir de las características sociodemográficas y de salud de la población, recopiladas de forma rutinaria en la ENDES.

Por los hallazgos se dedujo que la mayoría de los atributos relacionados con la salud materna e infantil (edad del niño, visitas prenatales por embarazo, momento del primer control prenatal, talla de la madre en centímetros), se relacionan con el padecimiento de anemia de los niños. Además, las características del hogar, como la altitud del conglomerado (en metros), mostraron una clara asociación con la incidencia de anemia.

Estos resultados difieren de los del estudio de Da Silva y cols.,⁽²¹⁾ sobre un de salud. Estos autores se enfocaron en aquellas variables que midieron la salud, y utilizaron como método estadístico la regresión de Poisson. Como resultado de ello, encontraron que en la población estudiada las prácticas inadecuadas de alimentación complementaria y la morbilidad fueron los principales predictores de anemia en la primera infancia.

Por otro lado, Gebremeskel y Tirote⁽²²⁾ aplicaron el modelo de regresión logística e identificaron como variables más influyentes para el control de la anemia: la lactancia materna exclusiva, el abordaje de la anemia materna, la fiebre infantil, la atención especial a los niños con bajo peso y la focalización en las regiones identificadas con alto riesgo de anemia. Molla y cols.⁽²³⁾ también utilizaron un modelo de regresión logística, y comprobaron que la visita de atención prenatal, la frecuencia de las comidas, la diversidad dietética, el bajo peso, el retraso del crecimiento y la inseguridad alimentaria se asociaron significativamente con la anemia.

Otros resultados parecidos a los del presente estudio fueron los de Shenton y cols.;⁽²⁴⁾ con un modelo de regresión logística multinomial, determinaron que las variables a tener en cuenta para la disminución de la anemia en niños son: la educación de las mujeres y las visitas de atención prenatal. En la India, Meena y cols.⁽¹⁹⁾ –quienes utilizaron árboles de decisión y minería de reglas de asociación– encontraron que los niveles de anemia de las madres y la ingesta de pastillas de hierro durante el embarazo son factores influyentes en los niveles de anemia en los niños.

A partir de una regresión lineal, Manikandan⁽²⁵⁾ encontró que el patrón de consumo (ingesta de alimentos) y la anemia materna son las principales causas de anemia entre la población infantil de los  distritos pobres de la India. Las diferencias en cuanto a la importancia de algunas variables respecto a las de otros estudios, estriban en que muchas de ellas no se tomaron en cuenta en el presente estudio y se aplicó otro modelo de estimación con niños también de edades diferentes. Durante la experimentación se construyeron varios procedimientos alternativos para predecir el riesgo de anemia infantil, basados en estas variables significativamente relacionadas.

Este estudio tuvo algunas limitaciones. Los procedimientos alternativos predictivos se establecieron a partir de datos de encuestas transversales demográficas y de salud familiar, por lo cual no se dispuso de información adicional sobre otras variables clínicas y dietéticas potencialmente relevantes. La incorporación de esas variables probablemente habría mejorado la precisión predictiva, dado que algunos atributos (diarreas y fiebre en los niños, durante las últimas dos semanas desde la fecha de la entrevista) fueron autoinformados, hubo posibilidades de sesgos de recuerdo. De los numerosos algoritmos de aprendizaje automático que pudieron aplicarse en este contexto, se eligió el del bosque de probabilidades por un juicio subjetivo.

CONCLUSIONES

Los mejores resultados se obtuvieron con los procedimientos alternativos B (todas las variables) y F (300 árboles, y variables seleccionadas). Aunque fueron balanceados, el procedimiento F tuvo un área bajo la curva de 70,09 %; por ello, sus porcentajes de especificidad y sensibilidad son más similares. Hay que tener en cuenta que al no utilizarse todas las variables –solo las más importantes–, se redujeron los cálculos. Para el indicador del área bajo la curva, todos los procedimientos superaron el valor mínimo (0,60), por lo que la calidad de las predicciones de la anemia fueron de regulares.

En cuanto a la especificidad –que mide la predicción de la clase que no es de interés (sin anemia)–, los procedimientos alternativos D y F obtuvieron los mayores valores (63,62 % y 63,62 %, respectivamente); de ahí que resultaran los mejores cuando se mejoraron los parámetros mediante la búsqueda en rejilla con balanceo. Para la sensibilidad, se midió la predicción de la clase de interés (con anemia), y los procedimientos A y C obtuvieron los mayores valores (71,87 % y 71,28 %, respectivamente). Los porcentajes resultaron mayores cuando se trabajó con el procedimiento original (A) sin balanceo.

Las cinco variables independientes más importantes para el mejor procedimiento (F) fueron: edad del niño, altitud del conglomerado, número de visitas prenatales por embarazo, momento del primer control prenatal y talla de la madre. Todas se deben tener en cuenta en el diseño y lanzamiento de futuras políticas públicas destinadas a la disminución del porcentaje de niños con anemia. El estudio aportó evidencias científicas acerca del uso de los algoritmos de aprendizaje automático para predecir la aparición de anemia en función de factores de riesgo comunes. Estas predicciones pueden servir de base al desarrollo de intervenciones de salud preventivas de la anemia infantil.

AGRADECIMIENTOS

Agradecimientos especiales a la escuela de Posgrado de la Universidad Nacional de Santa, y a mi familia por su apoyo incondicional.

REFERENCIAS BIBLIOGRÁFICAS

1. Instituto Nacional de Estadística e Informática (Perú). Encuesta Demográfica y de Salud Familiar. ENDES 2020 [Internet]. Lima: Instituto Nacional de Estadística e Informática; 2021 [citado 14 May 2021]. Disponible en: https://proyectos.inei.gob.pe/endes/2020/INFORME_PRINCIPAL_2020/INFORME_PRINCIPAL_ENDES_2020.pdf
2. Ministerio de Salud (Perú). Plan nacional para la reducción y control de la anemia materno infantil y la desnutrición crónica infantil y la desnutrición crónica infantil en el Perú: 2017-2021 [Internet]. Lima: MINSA; 2021 [citado 12 Abr 2017]. Disponible en: https://cdn.www.gob.pe/uploads/document/file/322898/Plan_nacional_para_la_reducci%C3%B3n_y_control_de_la_anemia_materno_infantil_y_la_desnutrici%C3%B3n_cr%C3%B3nica_infantil_en_el_Per%C3%BA__2017___2021._Documento_t%C3%A9cnico20190621-17253-s9ub98.pdf
3. Ministerio de Desarrollo e Inclusión Social (Perú). Plan multisectorial de lucha contra la anemia [Internet]. Lima: MIDIS; 2018 [citado 27 May 2018]. Disponible en: https://cdn.www.gob.pe/uploads/document/file/307159/plan-multisectorial-de-lucha-contra-la-anemia-v3.pdf
4. Sanou D, Ngnie-Teta I. Risk factors for anemia in preschool children in Sub-Saharan Africa. En: Silverberg DS, editor. Anemia [Internet]. Rijeka: InTech; 2012. p. 171-90. [citado 14 Feb 2012]. Disponible en: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1040.3665&rep=rep1&type=pdf
5. Balarajan Y, Ramakrishnan U, Özaltin E, Shankar AH, Subramanian SV. Anaemia in low-income and middle-income countries. The Lancet [Internet]. Ene 2012 [citado 3 Ago 2012];378(9809):2123-35. Disponible en: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1023.2792&rep=rep1&type=pdf
6. Saaka M, Galaa SZ. How is dietary diversity related to haematological status of preschool children in Ghana? Food Nutr Res [Internet]. Jun 2017 [citado 14 Jun 2017];61(1):1333389. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5475327/pdf/zfnr-61-1333389.pdf
7. Siekmans K, Receveur O, Haddad S. Can an integrated approach reduce child vulnerability to anaemia? Evidence from three African countries. PLoS ONE [Internet]. 2014 [citado Mar 2014];9(3):e90108. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3943899/pdf/pone.0090108.pdf
8. Véliz-Capuñay C. Aprendizaje automático. Análisis para la minería de datos y big data. Lima: Pontificia Universidad Católica del Perú; 2018.
9. Mahboob T, Irfan S, Karamat A. A machine learning approach for student assessment in e-learning using Quinlan’s C4.5, naive bayes and random forest algorithms. En: Proceedings of the 2016 19th International MultiTopic Conference, INMIC 2016. p. 1-8.
10. Ezzati M, López AD, Rodgers A, Murray CJL, editores. Comparative quantification of health risks: global and regional burden of disease attributable to selected major risk factors. Vol. 1 [Internet]. Geneva: WHO; 2004. [citado 18 Oct 2014]. Disponible en: https://apps.who.int/iris/bitstream/handle/10665/42770/9241580313_eng.pdf
11. Durán-Romo B. Comparación de metodologías de imputación aplicadas a ingresos laborales de la ENOE. Realidad, Datos y Espacio. Revista Internacional de Estadística y Geografía [Internet]. Dic 2019 [citado 18 Dic 2019];10(3):5-27. Disponible en: https://rde.inegi.org.mx/wp-content/uploads/2019/09/RDE29_art01_2c.pdf
12. Fernández-Vásquez RF. Regresión bayesiana con enlaces asimétricos para la clasificación de clientes con propensión a caer en mora en una entidad bancaria. Lima: Universidad Nacional Agraria La Molina; 2018 [citado 20 Feb 2018]. Disponible en: http://repositorio.lamolina.edu.pe/bitstream/handle/20.500.12996/3093/fernandez-vasquez-richard-fernando.pdf?sequence=3&isAllowed=y
13. Perez-Sánchez JM, Negrín-Hernández MA, García-García C, Gómez-Déniz E. Bayesian asymmetric logit model for detecting risk factors in motors ratemaking. Astin Bulletin. 2014;44(2):445-57.
14. Menze BH, Kelm BM, Masuch R, Himmelreich U, Bachert P, Petrich W, et al. Comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinformatics [Internet]. 2009 [citado 20 May 2014];10:213. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2724423/pdf/1471-2105-10-213.pdf
15. Kroese DP, Botev ZI, Taimre T, Vaisman R. Data science and machine learning. Mathematical and statistical methods. Boca Ratón: CRC Press; 2019.
16. Genuer R, Poggi JM. Random forest with R. En: Genuer R, Poggi JM. Random forest. London: Springer Nature, 2020. p. 33-55.
17. Khan JR, Chowdhury S, Islam H, Raheem E. Machine learning algorithms to predict the childhood anemia in Bangladesh. Journal of Data Science [Internet]. 2019 [citado 20 May 2019];17(1)195-218. Disponible en: https://www.jds-online.com/files/01%20No.09%20310%20Machine%20learning%20algorithms%20to%20predict%20the%20childhood%20anemia%20in%20Bangladesh.pdf
18. Alghamdi M, Al-Mallah M, Keteyian S, Brawner C, Ehrman J, Sakr S. Predicting diabetes mellitus using SMOTE and ensemble machine learning approach: The Henry Ford exercise testing (FIT) project. PloS One [Internet]. 2017 [citado 24 Jul 2017];12(7):e0179805. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5524285/pdf/pone.0179805.pdf
19. Meena K, Tayal DK, Gupta V, Fatima A. Using classification techniques for statistical analysis of anemia. Artif Intell Med. Mar 2019;94:138-52.
20. Khare S, Kavyashree S, Gupta D, Jyotishi A. Investigation of nutritional status of children based on machine learning techniques using Indian demographic and health survey data. Proc Comp Sci [Internet]. 2017 [citado 24 Jul 2017]115:338-49 Disponible en: https://reader.elsevier.com/reader/sd/pii/S187705091731894X?token=5D7B79CF5C71745C89B20E2D46EFE7FA649FA3E9ED92AED1E96C5BAD5AB8768649C171CDB95401D47D44C2C9ECCA1516yoriginRegion=us-east-1yoriginCreation=20220607134821
21. Santos-Da Silva LL, Wahib-Fawzi W, Augusto-Cardoso M. Factors associated with anemia in young children in Brazil. Plos One [Internet] 2018 [citado 25 Sep 2018];13(9):e0204504. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6155550/pdf/pone.0204504.pdf
22. Gebremeskel MG, Tirore LL. Factors associated with anemia among children 6-23 months of age in Ethiopia: a multilevel analysis of data from the 2016 Ethiopia Demographic and Health Survey. Pediatr Health Med Ther [Internet]. 2020 [citado 27 Jul 2020];11:347-57. Disponible en: https://www.dovepress.com/getfile.php?fileID=61509
23. Molla A, Egata G, Mesfin F, Arega M, Getacher L. Prevalence of anemia and associated factors among infants and young children aged 6-23 months in Debre Berhan Town, North Shewa, Ethiopia. J Nutr Metab [Internet]. 2020 [citado 27 Jul 2020];2020:2956129. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7768586/pdf/jnme2020-2956129.pdf
24. Shenton LM, Jones AD, Wilson ML. Factors associated with anemia status among children aged 6-59 months in Ghana, 2003-2014. Matern Child Health J [Internet]. Abr 2020 [citado 21 Abr 2020];24(4):483-502. Disponible en: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7078144/pdf/10995_2019_Article_2865.pdf
25. Manikandan AD. Factors Associated with anemia among women and children belonging to the scheduled castes and scheduled tribes in degraded districts of India. Indian Development Policy Review [Internet]. 2020 [citado 21 Abr 2020];1(1):43-66. Disponible en: https://www.esijournals.com/image/catalog/Journal%20Paper/IDPR/No%201%20(2020)/4_Manikandan.pdf

Conflictos de intereses

El autor declara que no existen conflictos de intereses.

Contribución del autor

La idea y parte del contenido de la obra es del único autor del artículo.

Financiación

Universidad Nacional del Santa. República del Perú.